Вычисление тройных интегралов: теория и примеры. Замена переменных в двойном интеграле

Примеры решений произвольных тройных интегралов.
Физические приложения тройного интеграла

Во 2-й части урока мы отработаем технику решения произвольных тройных интегралов , у которых подынтегральная функция трёх переменных в общем случае отлична от константы и непрерывна в области ; а также познакомимся с физическими приложениями тройного интеграла

Вновь прибывшим посетителям рекомендую начать с 1-й части, где мы рассмотрели основные понятия и задачу нахождения объема тела с помощью тройного интеграла . Остальным же предлагаю немного повторить производные функции трёх переменных , поскольку в примерах данной статьи мы будем использовать обратную операцию – частное интегрирование функции .

Кроме того, есть ещё один немаловажный момент: если у Вас неважное самочувствие, то прочтение этой странички по возможности лучше отложить. И дело не только в том, что сейчас возрастёт сложность вычислений – у большинства тройных интегралов нет надёжных способов ручной проверки, поэтому к их решению крайне нежелательно приступать в утомлённом состоянии. При пониженном тонусе целесообразно порешать что-нибудь попроще либо просто отдохнуть (я терпелив, подожду =)), чтобы в другой раз со свежей головой продолжить расправу над тройными интегралами:

Пример 13

Вычислить тройной интеграл

На практике тело также обозначают буквой , но это не очень хороший вариант, ввиду того, «вэ» «зарезервировано» под обозначение объёма.

Сразу скажу, чего делать НЕ НАДО. Не нужно пользоваться свойствами линейности и представлять интеграл в виде . Хотя если очень хочется, то можно. В конце концов, есть и небольшой плюс – запись будет хоть и длинной, но зато менее загромождённой. Но такой подход всё-таки не стандартен.

В алгоритме решения новизны будет немного. Сначала нужно разобраться с областью интегрирования. Проекция тела на плоскость представляет собой до боли знакомый треугольник:

Сверху тело ограничено плоскостью , которая проходит через начало координат. Предварительно, к слову, нужно обязательно проверить (мысленно либо на черновике) , не «срезает» ли эта плоскость часть треугольника. Для этого находим её линию пересечения с координатной плоскостью , т.е. решаем простейшую систему: – нет, данная прямая (на чертеже отсутствует) «проходит мимо», и проекция тела на плоскость действительно представляет собой треугольник.

Не сложен здесь и пространственный чертёж:

В действительности можно было ограничиться только им, поскольку проекция очень простая. …Ну, или только чертежом проекции, так как тело тоже простое =) Однако совсем ничего не чертить, напоминаю – плохой выбор.

Ну и, само собой, не могу не порадовать вас заключительной задачей:

Пример 19

Найти центр тяжести однородного тела, ограниченного поверхностями , . Выполнить чертежи данного тела и его проекции на плоскость .

Решение : искомое тело ограничено координатными плоскостями и плоскостью , которую в целях последующего построения удобно представить в отрезках : . Выберем «а» за единицу масштаба и выполним трёхмерный чертёж:

На чертеже уже поставлена готовая точка центра тяжести, однако, пока мы её не знаем.

Проекция тела на плоскость очевидна, но, тем не менее, напомню, как её найти аналитически – ведь такие простые случаи встречаются далеко не всегда. Чтобы найти прямую, по которой пересекаются плоскости нужно решить систему:

Подставляем значение в 1-е уравнение: и получаем уравнение «плоской» прямой :

Координаты центра тяжести тела вычислим по формулам
, где – объём тела.

Преобразование двойного интеграла от прямоугольных координат ,к полярным координатам
, связанных с прямоугольными координатами соотношениями
,
, осуществляется по формуле

Если область интегрирования
ограничена двумя лучами
,
(
), выходящими из полюса, и двумя кривыми
и
, то двойной интеграл вычисляют по формуле

.

Пример 1.3. Вычислить площадь фигуры, ограниченной данными линиями:
,
,
,
.

Решение. Для вычисления площади области
воспользуемся формулой:
.

.

1.2. Тройные интегралы

Основные свойства тройных интегралов аналогичны свойствам двойных интегралов.

В декартовых координатах тройной интеграл обычно записывают так:

.

Если
, то тройной интеграл по областичисленно равен объему тела:

.

Вычисление тройного интеграла

Пусть область интегрирования ограничена снизу и сверху соответственно однозначными непрерывными поверхностями
,
, причем проекция областина координатную плоскость
есть плоская область
(рис. 1.6).

.

Пример 1.4. Вычислить
, где- тело, ограниченное плоскостями:

Тройной интеграл в цилиндрических координатах

При переходе от декартовых координат
к цилиндрическим координатам
(рис. 1.9), связанных с
соотношениями
,
,
, причем

Область
, ограниченная кривой
, примет вид, или
, при этом полярный угол
. В итоге имеем

.

2. Элементы теории поля

Напомним предварительно способы вычисления криволинейных и поверхностных интегралов.

Вычисление криволинейного интеграла по координатам от функций, определенных на кривой , сводится к вычислению определенного интеграла вида

если кривая задана параметрическии
соответствует начальной точке кривой, а
- ее конечной точке.

Вычисление поверхностного интеграла от функции
, определенной на двусторонней поверхности, сводится к вычислению двойного интеграла, например, вида

если поверхность , заданная уравнением
, однозначно проецируется на плоскость
в область
. Здесь- угол между единичным вектором нормалик поверхностии осью
:

Требуемая условиями задачи сторона поверхности определяется выбором соответствующего знака в формуле (2.3).

Определение 2.1. Векторным полем
называется векторная функция точки
вместе с областью ее определения:

Векторное поле
характеризуется скалярной величиной –дивергенцией:

Определение 2.2. Потоком векторного поля
через поверхность называется поверхностный интеграл:

где - единичный вектор нормали к выбранной стороне поверхности, а
- скалярное произведение векторови.

Определение 2.3. Циркуляцией векторного поля

по замкнутой кривой называется криволинейный интеграл

где
.

Формула Остроградского-Гаусса устанавливает связь между потоком векторного поля через замкнутую поверхность и дивергенцией поля:

где - поверхность, ограниченная замкнутым контуром , а - единичный вектор нормали к этой поверхности. Направление нормали должно быть согласовано с направлением обхода контура .

Пример 2.1. Вычислить поверхностный интеграл

,

где - внешняя часть конуса
(
), отсекаемая плоскостью
(рис 2.1).

Решение. Поверхность однозначно проецируется в область
плоскости
, и интеграл вычисляется по формуле (2.2).

Область
есть круг
. Поэтому в последнем интеграле переходим к полярным координатам, при этом
,
:

Пример 2.2. Найти дивергенцию и ротор векторного поля
.

Решение. По формуле (2.4) получаем

Ротор данного векторного поля находим по формуле (2.5)

Пример 2.3. Найти поток векторного поля
через часть плоскости:
, расположенную в первом октанте (нормаль образует острый угол с осью
).

где
- проекция плоскостина
(рис. 2.4).

Пример 2.4. Вычислить поток векторного поля через замкнутую поверхность, образованную плоскостью
и частью конуса
(
) (рис. 2.2).

Решение. Воспользуемся формулой Остроградского-Гаусса (2.8)

.

Найдем дивергенцию векторного поля по формуле (2.4):

где
- объем конуса, по которому ведется интегрирование. Воспользуемся известной формулой для вычисления объема конуса
(- радиус основания конуса,- его высота). В нашем случае получаем
. Окончательно получаем

.

Пример 2.5. Вычислить циркуляцию векторного поля
по контуру , образованному пересечением поверхностей
и
(
). Проверить результат по формуле Стокса.

Решение. Пересечением указанных поверхностей является окружность
,
(рис. 2.1). Направление обхода выбирается обычно так, чтобы ограниченная им область оставалась слева. Запишем параметрические уравнения контура :

причем параметр изменяется отдо
. По формуле (2.7) с учетом (2.1) и (2.10) получаем

.

Применим теперь формулу Стокса (2.9). В качестве поверхности , натянутой на контур , можно взять часть плоскости
. Направление нормали
к этой поверхности согласуется с направлением обхода контура . Ротор данного векторного поля вычислен в примере 2.2:
. Поэтому искомая циркуляция

где
- площадь области
.
- круг радиуса
, откуда

Записывается тройной интеграл так:

Вычислить тройной интеграл - значит найти число, равное объёму тела V или, что то же самое - области V .

Практически каждый может понять смысл вычисления тройного интеграла "на своей шкуре". Точнее - "под шкурой", а ещё точнее - по своим органам дыхания - лёгким. Вне зависимости от того, знаете ли вы об этом или не знаете, в лёгких человека свыше 700 миллионов альвеол - пузырьковых образований, оплетённых сетью капилляров. Через стенки альвеол происходит газообмен. Поэтому можно рассуждать так: объём газа в лёкгих, можно представить в виде некоторой компактной области. А состоит этот объём из маленьких объёмов, сосредоточенных в альвеолах. Ключевую роль в этом сравнении играет именно огромное количество альвеол в лёгких: как мы увидим в следующем абзаце, через такое "огромное количество малостей" математически как раз и формулируется понятие тройного интеграла.

Почему именно тройной интеграл служит для нахождения объёма тела V ? Пусть область V разбита на n произвольных областей Δv i , причём под этим обозначением подразумевается не только каждая маленькая область, но и её объём. В каждой такой маленькой области выбрана произвольная точка M i , а f (M i ) - значение функции f (M ) в этой точке. Теперь будем максимально увеличивать число таких маленьких областей, а наибольший диаметр Δv i - наоборот, уменьшать. Можем составить интегральную сумму вида

Если функция f (M ) = f (x , y , z ) непрерывна, то будет существовать предел интегральных сумм вида, указанного выше. Этот предел и называется тройным интегралом .

В этом случае функция f (M ) = f (x , y , z ) называется интегрируемой в области V ; V - областью интегрирования; x , y , z - переменными интегрирования, dv (или dx dy dz ) - элементом объёма.

Вычисление тройного интеграла путём уменьшения кратности

Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычислению интегралов меньшей кратности.

Рассмотрим трёхмерную область V . Снизу и сверху (то есть по высоте) эта область ограничена поверхностями z = z 1 (x , y ) и z = z 2 (x , y ) . С боковых сторон (то есть по ширине) область ограничена поверхностями y = y 1 (x ) и y = y 2 (x ) . И, наконец, по глубине (если Вы смотрите на область в направлении оси Ox ) - поверхностями x = a и x = b

Чтобы применять переход к интегралам меньшей кратности, требуется, чтобы трёхмерная область V была правильной. Она правильна тогда, когда прямая, параллельная оси Oz , пересекает границу области V не более чем в двух точках. Правильными трёхмерными областями являются, например, прямоугольный параллелепипед, эллипсоид, тетраэдр. На рисунке ниже - прямоугольный параллелепипед, который встретится нам в первом примере на решение задач.

Чтобы наглядно представить отличие правильности от неправильности, добавим, что поверхности области по высоте у правильной области не должны быть вогнуты вовнутрь. На рисунке ниже - пример неправильной области V - однополостный гиперболоид, поверхность которого прямая, параллельная оси Oz (красного цвета), пересекает более чем в двух точках.

Мы будем рассматривать только правильные области.

Итак, область V - правильная. Тогда для любой функции f (x , y , z ) , непрерывной в области V , справедлива формула

Эта формула позволяет свести вычисление тройного интеграла к последовательному вычислению внутреннего определённого интеграла по переменной z (при постоянных x и y ) и внешнего двойного интеграла по двумерной области D .

Переходя от двойного интеграла к повторному, получаем следующую формулу для вычисления тройного интеграла:

Таким образом, для вычисления тройного интеграла требуется последовательно вычислить три определённых интеграла.

Вычисляются эти интегралы от самого внутреннего (по переменной z ) к самому внешнему (по переменной x ). Для удобства восприятия последовательности вычислений три "вложенных" интеграла можно записать так:

.

Из этой записи уже однозначно видно, что:

• сначала нужно интегрировать функцию f (x , y , z ) по переменной z , а в качестве пределов интегрирования взять уравнения z = z 1 (x , y ) и z = z 2 (x , y ) поверхностей ограничивающих область V снизу и сверху;
• y y = y 1 (x ) и y = y 2 (x ) поверхностей, ограничивающих область V с боковых сторон;
• получившийся на предыдущем шаге результат интегрировать по переменной x , а в качестве пределов интегрирования взять уравнения x = a и x = b поверхностей, ограничивающих область V по глубине.

Пример 1. Пусть от тройного интеграла можно перейти к повторному интегралу

-

последовательности трёх определённых интегралов. Вычислить этот повторный интеграл.

Решение. Вычисление повторного интеграла всегда начинается с последнего интеграла:

.

Вычислим второй интеграл - по переменной y :

.

x :

.

Ответ: данный повторный интеграл и соответствующий ему тройной интеграл равен 10.

Пример 2. Вычислить тройной интеграл

,

где V - параллелепипед, ограниченный плоскостями x = − 1 , x = + 1 , y = 0 , y = 1 , z = 0 , z = 2 .

Решение. Пределы интегрирования для всех трёх определённых интегралов однозначно заданы уравнениями поверхностей, ограничивающих параллелепипед. Поэтому сразу сводим данный тройной интеграл к последовательности трёх определённых интегралов:

.

z

.

Вычисляем интеграл "в серединке" - по переменной y . Получаем;

.

Теперь вычисляем самый внешний интеграл - по переменной x :

Ответ: данный тройной интеграл равен -2.

Пример 3. Вычислить тройной интеграл

,

где V x + y + z = 1 и координатными плоскостями x = 0 , y = 0 , z = 0 . Область V проецируется на плоскость xOy в треугольник D , как показано на рисунке ниже.

Решение. Расставим сначала пределы интегрирования. Для интеграла по переменной z нижний предел интегрирования задан однозначно: z = 0 . Чтобы получить верхний предел, выразим z из x + y + z = 1 . Получаем 1 − x − y . Для интеграла по переменной y нижний предел интегрирования задан однозначно: y = 0 . Для получения верхнего предела выразим y из x + y + z = 1 , считая при этом, что z = 0 (так как линия расположена в плоскости xOy ). Получаем: 1 − x .

Сводим данный тройной интеграл к последовательности трёх определённых интегралов:

.

Вычисляем самый внутренний интеграл - по переменной z , считая икс и игрек константами. Получаем:

.

y . Получаем:

x :

Ответ: данный тройной интеграл равен 1/8.

Вычислить тройной интеграл самостоятельно, а затем посмотреть решение

Пример 4. Вычислить тройной интеграл

,

где V - пирамида, ограниченная плоскостью x + y + z = 1 и координатными плоскостями x = 0 , y = 0 , z = 0 .

Расстановка пределов интегрирования при переходе к последовательности трёх интегралов

Бывает, что студенты, у которых не вызывает особых трудностей непосредственное вычисление интегралов, не могут освоиться в расстановке пределов интегрирования при переходе от тройного интеграла к последовательности трёх определённых интегралов. В этом деле действительно требуется некоторая натренированность. В первом примере область интегрирования V представляла собой параллелепипед, с которым всё понятно: со всех сторон его ограничивают плоскости, а значит, пределы интегрирования однозначно заданы уравнениями плоскостей. Во втором примере - пирамида: здесь уже требовалось чуть больше подумать и выразить один из пределов из уравнения. А если область V ограничивают не плоские поверхности? Нужно, конечно, определённым образом осмотреть область V .

Начнём с примера "пострашнее", чтобы почувствовать "обстановку, приближенную к боевой".

Пример 5. Расставить пределы интегрирования при переходе от тройного интеграла, в котором область V - эллипсоид

.

Решение. Пусть центр эллипсоида - начало координат, как показано на рисунке выше. Посмотрим на эллипсоид снизу. Снизу его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена ниже плоскости xOy z и полученное выражение со знаком минус будет нижним пределом интегрирования по переменной z :

.

Теперь посмотрим на эллипсоид сверху. Здесь его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена выше оси xOy . Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение будет верхним пределом интегрирования по переменной z :

.

Проекцией эллипсоида на плоскость xOy является эллипсоид. Его уравнение:

Чтобы получить нижний предел интегрирования по переменной y , нужно выразить y из уравнения эллипсоида и взять полученное выражение со знаком минус:

.

Для верхнего предела интегрирования по переменной y то же выражение со знаком плюс:

Что касается интегрирования по переменной x , то область V ограничена по глубине плоскостями. Следовательно, пределы интегрирования по переменной x можно представить как координаты задней и передней границ области. В случае эллипсоида ими будут взятые с отрицательным и положительным знаками величины длин полуоси a : x 1 = − a и x 2 = a .

Таким образом, последовательность интегралов для вычисления объёма эллипсоида следующая:

,

где "игрек первое", "игрек второе", "зет первое" и "зет второе" - полученные выше выражения. Если у Вас есть желание и отвага вычислить этот интеграл и, таким образом, объём эллипсоида, то вот ответ: 4πabc /3 .

Следующие примеры - не такие страшные, как только что рассмотренный. При этом они предполагают не только расстановку пределов интегрирования, но и вычисление самого тройного интеграла. Проверьте, чему вы научились, следя за решением "страшного" примера. Думать при расстановке пределов всё равно придётся.

Пример 6. Вычислить тройной интеграл

если область интегрирования ограничена плоскостями x + y = 1 , x + 2y = 4 , y = 0 , y = 1 , z = 1 , z = 5 .

Решение. "Курортный" пример по сравнению с примером 5, так как пределы интегрирования по "игрек" и "зет" определены однозначно. Но придётся разобраться с пределами интегрирования по "иксу". Проекцией области интегрирования на плоскость xOy является трапеция ABCD .

В этом примере выгоднее проецировать трапецию на ось Oy , иначе, чтобы вычислить тройной интеграл, на придётся разделить фигуру на три части. В примере 4 мы начинали осмотр области интегрирования снизу, и это обычный порядок. Но в этом примере мы начинаем осмотр сбоку или, если так проще, положили фигуру набок и считаем, что смотрим на неё снизу. Можем найти пределы интегирования по "иксу" чисто алгебраически. Для этого выразим "икс" из первого и второго уравнений, данных в условии примера. Из первого уравения получаем нижний предел 1 − y , из второго - верхний 4 − 2y . Сведём данный тройной интеграл к последовательности трёх определённых интегралов:

.

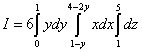Внимание! В этом примере самый внешний интеграл - не по переменной "икс", а по переменной "игрек", а "средний" - по переменной "икс"! Здесь мы применили смену порядка интегрирования, с которой ознакомились при изучении двойного интеграла. Это связано с тем, что, как уже говорилось, мы начали осмотр области интегрирования не снизу, а сбоку, то есть спроецировали её не на ось Ox , на на ось Oy .

Вычисляем самый внутренний интеграл - по переменной z , считая икс и игрек константами. Получаем:

Вычисляем средний интеграл - по переменной x . Получаем:

.

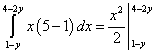Наконец, вычисляем самый внешний интеграл - по переменной y :

Ответ: данный тройной интеграл равен 43.

Пример 7. Вычислить тройной интеграл

,

если область интегрирования ограничена поверхностями x = 0 , y = 0 , z = 2 , x + y + z = 4 .

Решение. Область V (пирамида MNRP ) является правильной. Проекцией области V на плоскость xOy является треугольник AOB .

Нижние пределы интегрирования по всем переменным заданы в условии примера. Найдём верхний предел интегирования по "иксу". Для этого выразим "икс" из четвёртого уравнения, считая "игрек" равным нулю, а "зет" равным двум. Получаем x = 2 . Найдём верхний предел интегирования по "игреку". Для этого выразим "игрек" из того же четвёртого уравнения, считая "зет" равным двум, а "икс" - переменной величиной. Получаем y = 2 − x . И, наконец, найдём верхний предел интегрирования по переменной "зет". Для этого выразим "зет" из того же четвёртого уравнения, считая "игрек" и "зет" переменными величинами. Получаем z = 4 − x − y .

Сведём данный тройной интеграл к последовательности трёх определённых интегралов:

.

Вычисляем самый внутренний интеграл - по переменной z , считая икс и игрек константами. Получаем:

.

Вычисляем средний интеграл - по переменной y . Получаем:

.

Вычисляем самый внешний интеграл - по переменной x и окончательно находим данный тройной интеграл:

Ответ: данный тройной интеграл равен 2.

Замена переменных в тройном интеграле и цилиндрические координаты

Если проекцией области интегрирования на какую-либо из координатных плоскостей является круг или часть круга, то тройной интеграл проще вычислисть, перейдя к цилиндрическим координатам. Цилиндрическая система координат является обобщением полярной системы координат на пространство. В системе цилиндрических координат точка M характеризуется тремя величинами (r , φ , z ), где r - расстояние от начала координат до проекции N точки M на плоскость xOy , φ - угол между вектором ON и положительным направлением оси Ox , z - аппликата точки M (рисунок ниже).

Прямоугольные координаты x , y , z с цилиндрическими координатами r , φ , z связывают формулы

x = r cosφ ,

y = r sinφ ,

z = z .

Для того, чтобы в тройном интеграле перейти к цилиндрическим координатам, нужно подынтегральную функцию выразить в виде функции переменных r , φ , z :

То есть переход от прямогольных координат к цилиндрическим осуществляется следующим образом:

Тройной интеграл в цилиндрических координатах вычисляется так же как и в декартовых прямоугольных координатах, путём преобразования в последовательность трёх определённых интегралов:

Пример 8. Вычислить тройной интеграл

переходом к цилиндрическим координатам, где V - область, ограниченная поверхностями и .

Решение. Так как область V на плоскость xOy проектируется в круг , то координата φ изменяется в пределах от 0 до 2π , а координата r - от r =0 до r =1. Постоянному значению в пространстве соответствует цилиндр . Рассматривая пересечение этого цилиндра с областью V , получаем изменение ординаты z от z = r ² до z = 1 . Переходим к цилиндрическим координатам и получаем.

Пусть дано материальное тело, представляющее собой пространственную область П, заполненную массой. Требуется найти массу m этого тела при условии, что в каждой точке Р € П известна плотность распределения масс. Разобьем область П на неперекрывающиеся кубируемые (т. е. имеющие объем) части с объемами соответственно. В каждой из частичных областей ft* выберем произвольнуюточкуР*. Примем приближенно, что в пределах частичной области ft* плотность постоянна и равна /*(Р*). Тогда масса Атк этой части тела выразится приближенным равенством Атпк а масса всего тела будет приближенно равна Тройной интеграл Свойства тройных интегралов Вычисление тройного интеграла в декартовых координатах Вычисление тройного интеграла в цилиндрических и сферических координатах Пусть d - наибольший из диаметров частичных областей Если при d -* 0 сумма (1) имеет конечный предел, не зависящий ни от способа разбиения области ft на частичные подобласти, ни от выбора точек Р* € ft*, то этот предел принимается за массу m заданного тела, Пусть в замкнутой кубируемой области ft определена ограниченная функция Разобьем ft на п непересекающихся кубируемых частей а их объемы обозначим через соответственно. В каждой частичной подобласти П* произвольным образом выбираем точку Рк(хк, ук, zk) и составляем интегральную сумму Пусть d - наибольший из диаметров частичных областей Определение. Если при d О интегральные суммы а имеют предел, не зависящий ни от способа разбиения области Л на частичные подобласти П*, ни от выбора точек Рк € П*, то этот предел называется тройнич интегралам от функции f(x} у, z) по области Q и обозначается символом Теорема 6. Если функция f(x, у, z) непрерывна в замкнутой кубируемой области П, то она интегрируема в этой области. Свойства тройных интегралов Свойства тройных интегралов аналогичны свойствам двойных интегралоа Перечислим основные из них. Пусть функции интегрируемы в кубируемой области Л. 1. Линейность. При этом функция называется интегрируемой в области Q. Таким образом, по определению имеем Возвращаясь к задаче о вычислении массы тела, замечаем, что предел (2) есть тройной интеграл огт фуншни р(Р) по области П. Значит, Здесь dx dy dz - элемент объема dv в прямоугольных координатах. где а и (3 - произвольные вещественные постоянные. всюду в области П,то 3. Если /(Р) = 1 в области П, то п где V - объем области Q. Если функция /(Р) непрерывна в замкнутой кубируемой области ft и М и т - ее наибольшее и наименьшее значения в ft, то где V - объем области ft. 5. Аддитивность. Если область ft разбита на кубируемые области без общих внутренних точек и f{P) интегрируема в области ft, то f(P) интегрируема на каждой из областей ft| и ft2, причем 6. Теорема о среднем значении. Теореме 7 (о среднем значении). Если функция f(P) непрерывна в замкнутой кубируемой области ft, то найдется тонка Рс € ft, такая, что будет справедлива формула где V - объем области ft (напомним, что область - связное множество). § 7. Вычисление тройного интеграла в декартовых координатах Как и при вычислении двойных интегралов, дело сводится к вычислению повторных интегралов. Предположим, что функция непрерывна в некоторой области ft. 1-й случай. Область ft представляет собой прямоугольный параллелепипед проектирующийся на плоскость yOz в прямоугольник i2; Тогда получим Заменяя двойной интеграл через повторный, окончательно получим Таким образом, в случае, когда область П - прямоугольный параллелепипед, мы свели вычисление тройного интеграла к последовательному вычислению трех обыкновенных интегралов. Формулу (2) можно переписать в виде где прямоугольник есть ортогональная проекция параллелепипеда П на плоскость хОу. 2-й случай. Рассмотрим теперь область Q такую, что ограничивающая ее поверхность 5 пересекается любой прямой, параллельной оси Oz, не более чем в двух точках или по целому отрезку (рис.22). Пусть z = tpi(x,y) уравнение поверхности 5, ограничивающей область П снизу, а поверхность S2, ограничивающая область П сверху, имеет уравнение z = у). Пусть обе поверхности S\ и S2 проектируются на одну и ту же область плоскости хОу. Обозначим ее через D, а ограничивающую ее кривую через L. Остальная часть границы 5 тела Q лежит на цилиндрической поверхности с образующими, параллельными оси Oz, и с кривой L в роли направляющей. Тогда по аналогии с формулой (3) получим Если область D плоскости хОу представляет собой криволинейную трапецию, ограниченную двумя кривыми, то двойной интеграл в формуле (4) можно свести к повторному, и мы получим окончательно Эта формула является обобщением формулы (2). Рис-23 Пример. Вычислить объем тетраэдра, ограниченного плоскостями Проекцией тетраэдра на плоскость хОу служит треугольник, образованный прямыми так что х изменяется от 0 до 6, а при фиксированном х (0 ^ х ^ 6) у изменяется от 0 до 3 - | (рис. 23). Если же фиксированы и х, и у, то точка может перемещаться по вертикали от плоскости до плоскости меняется в пределах от 0 до 6 - х - 2у. По формуле получаем §8. Вычисление тройного интеграла в цилиндрических и сферических координатах Вопрос о замене переменных в тройном интеграле решается таким же путем, как и в случае двойного интеграла. Пусть функция /(ж, у, z) непрерывна в замкнутой кубируемой области ft, а функции непрерывны вместе со своими частными производными первого порядка в замкнутой кубируемой области ft*. Предположим, что функции (1) устанавливают взаимнооднозначное соответствие между всеми точками rj, {) области ft*, с одной стороны, и всеми точками (ж, у, z) области ft - с другой. Тогда справедлива формула замены переменных в тройном интеграле - где - якобиан системы функций (1). На практике при вычислении тройных интеграловчасто пользуются заменой прямоугольных координат цилиндрическими и сферическими координатами. 8.1. Тройной интеграл в цилиндрических координатах В цилиндрической системе координат положение точки Р в пространстве определяется тремя числами р, где р и (р - полярные координаты проекции Р1 точки Р на плоскость хОу, a z - аппликата точки Р (рис.24). Числа называются цилиндрическими координатами точии Р. Ясно, что В системе цилиндрических координат координатные поверхности Тройной интеграл Свойства тройных интегралов Вычисление тройного интеграла в декартовых координатах Вычисление тройного интеграла в цилиндрических и сферических координатах соответственно описывают: круговой цилиндр, ось которого совпадает с осью Oz, полуплоскость, примыкающую к оси Oz, и плоскость, параллельную плоскости хОу. Цилиндрические координаты связаны с декартовыми следующими формулами (см. рис. 24). Для системы (3), отображающей область ft на область имеем и формула (2) перехода от тройного интеграла в прямоугольных координатах к интегралу в цилиндрических координатах принимает вид (4) Выражение называется элементом объема в цилиндрических координатах. Это выражение для элемента объема может быть получено и из геометрических соображений. Разобьем область П на элементарные подобласти координатными поверхностями и вычислим объемы полученных криволинейных призм (рис. 25). Видно, что Отбрасывая бесконечно малую величину более высокого порядка, получаем Это позволяет принять за элемент объема в цилиндрических координатах следующую величину Пример 1. Найти объем тела, ограниченного поверхностями 4 В цилиндрических координатах заданные поверхности будут иметь уравнения (см. формулы (3)). Эти поверхности пересекаются по линии г, которая описывается системой уравнений (цилиндр), (плоскость), рис 26 а ее проекция на плоскость хОу системой Таким образом, Искомый объем вычисляется по формуле (4), в которой. Тройной интеграл в сферических координатах В сферической системе координат положение точки Р(х, у, z) в пространстве определяется тремя числами, где г - расстояние от начала координат до точки угол между осью Ох и проекцией радиуса-вектора ОР точки Р на плоскость хОу, а в - угол между осью Oz и радиусом-вектором ОР точки Р, отсчитываемый от оси Oz (рис. 27). Ясно, что. Координатные поверхности в этой системе координат: г = const - сферы с центром в начале координат; ip = constполуплоскости, исходящие из оси Oz; в = const - круговые конусы с осью Oz. Рис. 27 Из рисунка видно, что сферические и декартовы координаты связаны следующими соотношениями Вычислим якобиан функций (5). Имеем Следовательно, и формула (2) принимает вид Элемент объема в сферических координатах - Выражение для элемента объема можно получить и из геометрических соображений. Рассмотрим элементарную область в пространстве, ограниченную сферами радиусов г и г + dr, конусами в и в + d$ и полуплоскостями Приближенно эту область можно считать прямоугольным параллелепипедом с измерениями. Тогда Тройной интеграл Свойства тройных интегралов Вычисление тройного интеграла в декартовых координатах Вычисление тройного интеграла в цилиндрических и сферических координатах Пример 2. Найти объем выпуклого тела Q, вырезаемого из конуса концентрическими сферами -4 Переходим к сферической системе координат Из первых двух уравнений видно, что. Из третьего уравнения находим пределы изменен угла 9: откуда